Vienas iš Python lstsq() metodų naudojamas rasti žinomos tiesinės lygties ax=b regresijos tiesę, kuri geriausiai atitinka šią lygtį. Tai reiškia, kad turite nustatyti liniją, kuri tinkamai rodo ryšį tarp x ir y taškų, jei jūsų duomenys rodo, kad toks yra. Tiesė tarp abiejų taškų yra žinoma kaip regresijos linija, kai ji naudojama rasti mažiausią kvadratą per šią lygtį, ax=b.
Sintaksė:
Pradėkime mokytis funkcijos linalg.lstsq() įgyvendinimo stiliaus. Pirma, parašome bibliotekos pavadinimą, kurį naudojame Python, kuris yra „numpy“. Tada sujungiame linalg() funkciją ir lstsq() funkciją. Funkcija linalg() reiškia tiesinę algebrą. Jis visada naudojamas su lstsq() funkcija, nes tai linijinė algebrinė išraiška. Po to perduodame argumentus funkcijų skliausteliuose.

Parametrai:
Supraskime funkcijos linalg.lstsq() parametrus:
1 taškas: Tai koeficientų matrica.
2 taškas: Šioje matricoje arba masyve yra priklausomi kintamieji.
rcond: Jo duomenų tipas yra float. Rcond santykis yra mažesnių taško_1 vienaskaitos verčių riba. Jei vienaskaitos reikšmė yra mažesnė nei rcond padauginta iš didžiausio taško_1 vienaskaitos elemento, nustatant rangą ji laikoma nuliu.
Grąžinimo vertė:
Mainais gauname mažiausią žinomo kintamojo x kvadratą lygtyje ax=b.
1 pavyzdys:
Pradėkime įgyvendinti savo pirmąjį mažiausiojo kvadrato metodo Python bibliotekos NumPy pavyzdį. Pirma, mums reikia Python kompiliatoriaus, kad galėtume jame koduoti. Atidarykite kompiliatorių. Taip pat turite įdiegti „NumPy“ biblioteką, nes naudojame vieną iš „NumPy“ funkcijų, kuri yra lstsq () funkcija. Tada turite importuoti „NumPy“ paketą. Pirmiausia parašykite raktinį žodį „importas“, kuris praneša kompiliatoriui, kad ketiname importuoti paketą. Tada turime parašyti paketo pavadinimą, kurį naudojame funkcijoje, kuri yra „numpy“. Tada mes taip pat parašome alternatyvų NumPy pavadinimą „np“, nes daugelis programuotojų naudoja šį metodą. Tai geras programavimo metodas ir taupo laiką.
Importavę paketą, pradedame rašyti tikrąją kodo eilutę, kurią norime padaryti. Pirmiausia spausdiname pranešimus, kad vartotojas galėtų lengvai suprasti, ką darome pavyzdyje, naudodami teiginį print(). Sukuriame vienmatį masyvą „A“ naudodami funkciją array() ir išspausdiname jį iškviesdami print() sakinį. Tada mes sukuriame kitą vienmatį masyvą „B“ naudodami funkciją „masyvo()“ ir išspausdiname jį naudodami funkciją „print().
importuoti nelygus kaip pvz.spausdinti ( Mažiausio kvadrato metodo įgyvendinimas naudojant NumPy: )
A = pvz. masyvas ( [ 1 , du , 1 , 1 , 1 , du , du , 1 , 1 ] )
spausdinti ( “ \n Masyvas A yra: ' , A )
B = pvz. masyvas ( [ 4 , 3 , 5 , 4 , du , 3 , 6 , 3 , du ] )
spausdinti ( “ \n Masyvas B yra: ' , B )
X = pvz. sėmenų . lst kv ( pvz. vstack ( [ A , pvz. vieni ( tik ( A ) ) ] ) . T , B , rcond = Nė vienas ) [ 0 ]
spausdinti ( “ \n Mažiausias kvadratas yra: ' , X )
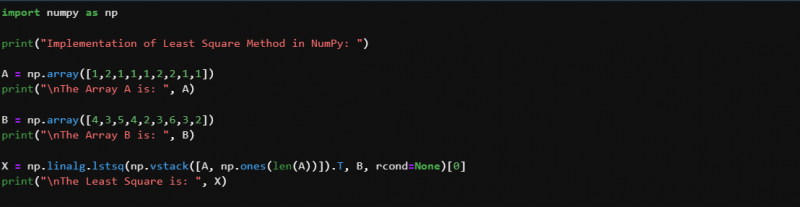
Sukūrę abu taškus A ir B, įgyvendiname lstsq() funkciją. Tačiau pirmiausia naudojame funkciją vstack () norėdami sukrauti „A“ elementus pagal seką. Tada paimame masyvo „A“ perkėlimą. Tada perduodame funkciją vstack() kaip pirmąjį funkcijos lstsq() argumentą. Antrasis argumentas yra „B“ masyvas, o trečiasis argumentas yra „rcond“, kuriame rcond reikšmę nustatome kaip „none“. Tada visą funkciją išsaugome kitame masyve, pavadintame „x“, kuris parodo, kad tai yra žinoma kintamojo tiesinė lygtis, ax=b. Po to rodome rezultatus, todėl naudojame print () sakinį ir perduodame jame „x“ masyvą.

2 pavyzdys:
Dabar pradėkime įgyvendinti kitą NumPy mažiausių kvadratų pavyzdį. Mes visada pirmiausia importuojame biblioteką, kurią naudojame programoje, kuri yra NumPy. Pirmiausia parašome raktinį žodį „importuoti“, kad paketas būtų programoje. Taip pat parašome paketo pavadinimą, kuris yra „numpy“, o tada jo slapyvardį „np“. Tada iškviečiame print() metodą, kad galėtume parodyti mažiausiųjų kvadratų pakartotinį pranešimą, kad geriau suprastume vartotoją.
Tada sukuriame masyvo pavadinimą „x_axis“ ir išsaugome jame masyvą naudodami arange () funkciją. Tada spausdiname naudodami print() metodą. Tada sukuriame kitą masyvo pavadinimą „y_axis“ ir saugome jame masyvą, kurį sukūrėme šioje iliustracijoje.
Sukūrę abu masyvus, mes įdiegiame one() metodą x_axis masyve ir išsaugome jį kitame masyve, pavadintame 'masyvo_a'. Tada mes taip pat spausdiname šį masyvą. Sukuriame kitą masyvą pavadinimu „arg_reg_line“ ir jame įdiegiame linalg.lstsq() funkciją. Tada mes perduodame parametrus šiai funkcijai, kad gautume mažiausius kvadratus tarp dviejų masyvų ar taškų. Pirmasis parametras yra tai, kad mes transponuojame masyvą_a. Antrasis parametras yra antrasis taškas, kuris yra y_ašis. Tada turime „rcond“, kuriame yra „none“ reikšmė. Tada rodome masyvą naudodami print () metodą.
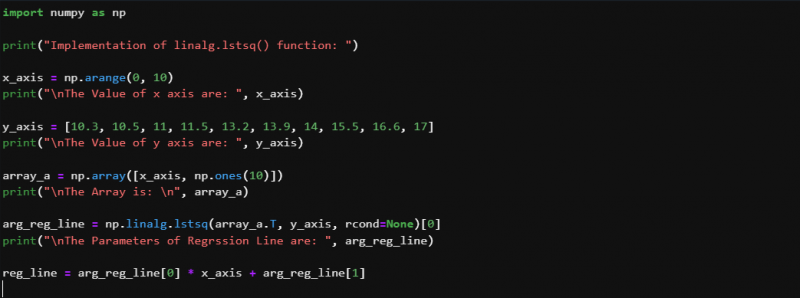
importuoti nelygus kaip pvz.spausdinti ( 'Funkcijos linalg.lstsq() įgyvendinimas: ' )
x_ašys = pvz. aranžuoti ( 0 , 10 )
spausdinti ( “ \n X ašies reikšmės yra: , x_ašys )
y_ašis = [ 10.3 , 10.5 , vienuolika , 11.5 , 13.2 , 13.9 , 14 , 15.5 , 16.6 , 17 ]
spausdinti ( “ \n Y ašies reikšmės yra: ' , y_ašis )
masyvas_a = pvz. masyvas ( [ x_ašys , pvz. vieni ( 10 ) ] )
spausdinti ( “ \n Masyvas yra: \n “ , masyvas_a )
arg_reg_line = pvz. sėmenų . lst kv ( masyvas_a. T , y_ašis , rcond = Nė vienas ) [ 0 ]
spausdinti ( “ \n Regrsijos linijos parametrai yra šie: , arg_reg_line )
reg_line = arg_reg_line [ 0 ] * x_axis + arg_reg_line [ 1 ]
importuoti matplotlib. pyplot kaip plt
plt. sklypas ( x_ašys , reg_line , 'r-' )
plt. sklypas ( x_ašys , y_ašis , 'o' )
plt. titulą ( 'Tiesinė regresijos linija' )
plt. xlabel ( 'X ašis' )
plt. etiketė ( 'Y ašis' )
plt. Rodyti ( )
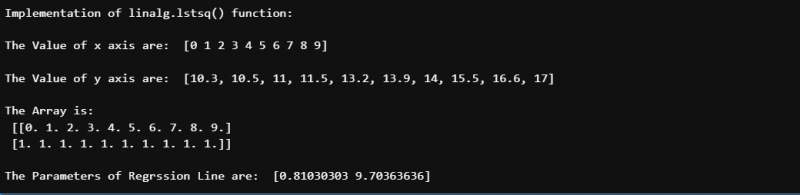
Štai anksčiau įdiegto pavyzdžio išvestis:
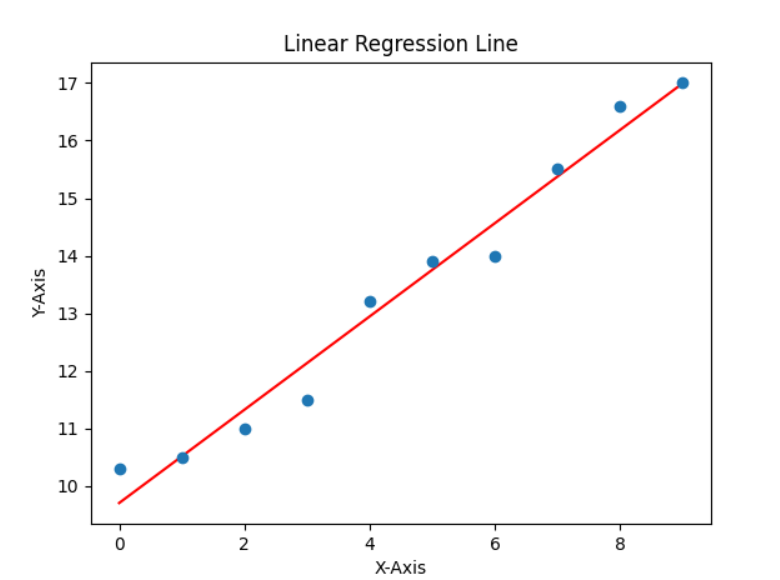
Importuojame kitą „NumPy“ paketą, kuris yra „matplotlib“ paketas, naudojamas diagramai nubraižyti. Tada nubraižome x_ašies reikšmes ir y_ašies_reikšmes. Toliau nustatome grafiko pavadinimą ir etiketes. Galiausiai grafiką rodome naudodami show() metodą.

Čia yra norimas pateikto pavyzdžio grafikas:
Išvada
Šiame straipsnyje sužinojome, kas yra mažiausias kvadratas ir kaip gauname nežinomo kintamojo x linalg.lstsq() naudojant tiesinę lygtį ax=b. Naudojome kelias NumPy funkcijas, kad surastume mažiausius kvadratus, ir įgyvendinome keletą pavyzdžių su išsamiais paaiškinimais, kad geriau suprastume vartotoją.